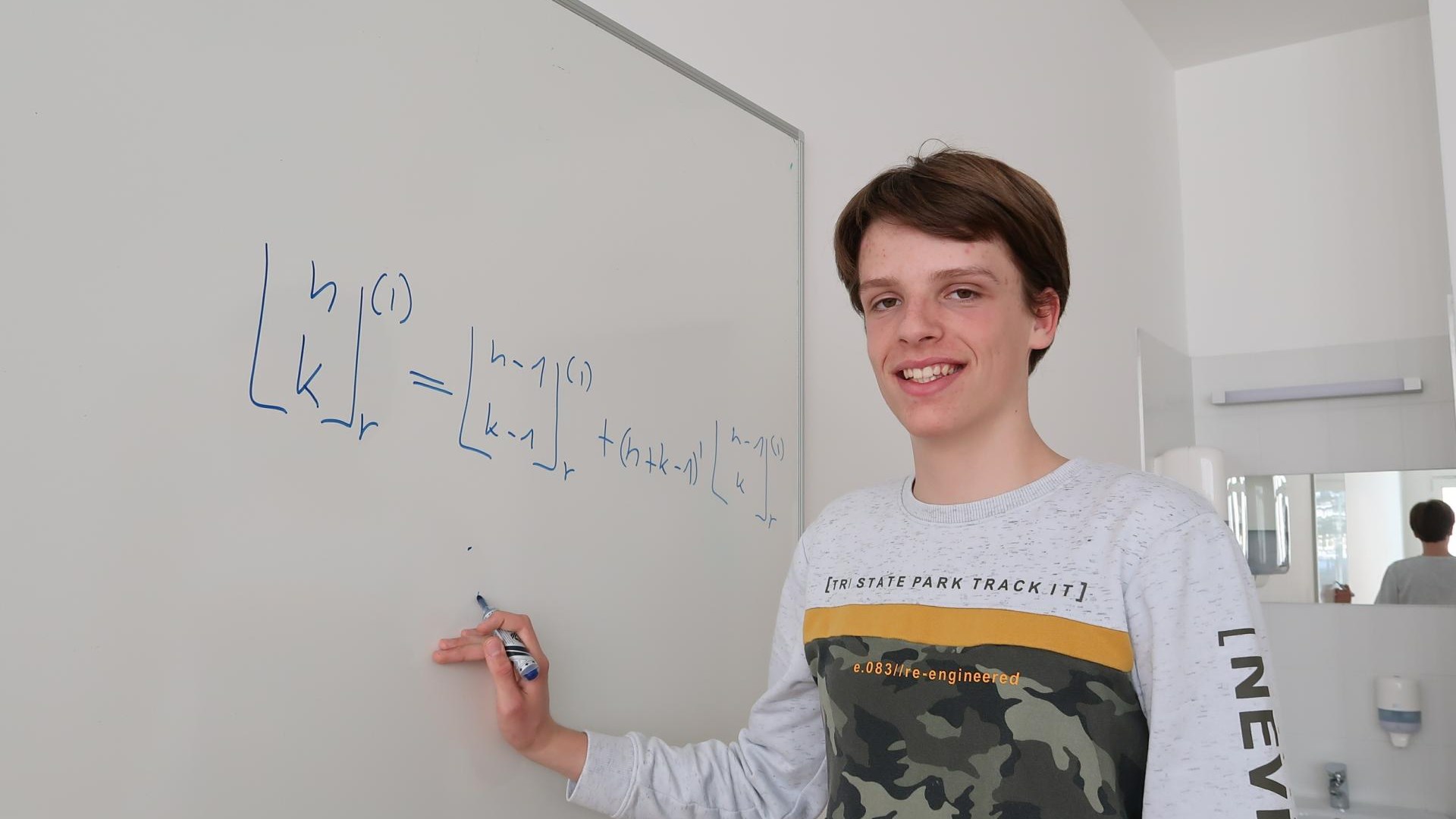“Fico satisfeito e me sinto bem quando vejo que artigos de professores e pesquisadores de destaque são publicados na mesma edição da revista ao lado da minha”, diz o humilde, mas extremamente independente e persistente jovem matemático, para quem a sexta série do ensino fundamental foi um ponto de virada e – por mais estranho que pareça – uma epidemia e a migração da vida online. Durante o ensino a distância, ele estudou rapidamente o material escolar e depois passou o tempo pesquisando livros didáticos de matemática. Primeiro, ele refez os livros do ensino fundamental, depois se deparou com o livro de matemática do ensino médio de sua mãe e, quando não encontrou nada de novo nele, juntou-se a palestras online para alunos de matemática e seminários de doutorado. Ele concorda que a epidemia realmente lhe trouxe sorte – hoje ele provavelmente não teria mais a oportunidade de assistir a palestras online, mas naquela época ele conseguia “esgueirar-se” para dentro delas completamente despercebido. Ele preenchia seus dias com horários de aulas online enquanto sua mãe e seu pai tentavam convencê-lo de que havia mais na vida do que matemática. Ar puro, por exemplo, ou amigos e diversão.

Ele não deixou nada incomodá-lo. Ele foi atraído pela combinatória. “Quanto mais difícil, mais interessante é”, ele ri e diz que a combinatória costuma ser considerada um dos ramos mais difíceis da matemática, pois combina muitos conhecimentos matemáticos – desde análises, integrais, derivações até lógica. Combinatória, diz ele, não é apenas que mulheres com um monte de pares de sapatos, saias e jaquetas podem calcular quantas maneiras podemos nos vestir de manhã, mas muito mais. “A combinatória enumerativa, um dos três ramos da combinatória que me atraiu, é, por exemplo, muito útil em genética e biologia. Com sua ajuda, podemos prever a probabilidade de nascer uma prole com características definidas com precisão. Alguns sistemas de navegação são baseados na teoria dos grafos, outro ramo da combinatória. Um dos meus matemáticos favoritos, Leonhard Euler, por exemplo, provou uma importante descoberta usando o exemplo de uma ilha no rio no meio de Kaliningrado, na Rússia. Várias pontes levavam à ilha , e os habitantes da cidade, perseguindo o tédio, se entretinham com a ideia de como fazer uma rota fechada que cruzaria todas as pontes apenas uma vez. Euler descobriu que tal caminho não existe. Pelo menos uma ponte ou entroncamento tinha que ser cruzados duas vezes. Hoje, essa descoberta também é útil em sistemas de computador”, o garoto de quatorze anos enumera os aspectos úteis da combinatória. Ele sorri que com a ajuda da combinatória também poderíamos calcular como dispor os convidados nas mesas da coroação do rei Carlos III sem que eles se olhassem.

Enquanto monitorava as aulas online, ele também se deparou com uma ministrada pelo professor da Faculdade de Matemática e Física de Ljubljana, Dr. Marko Petkovšek, um bom conhecedor de combinatória. Naquela época, o aluno da sétima série criou coragem para escrever um e-mail para ele e, ao mesmo tempo, enviou-lhe duas ideias interessantes que ele mesmo teve. “O professor ficou satisfeito. Não porque eu descobri algo novo, como pensei a princípio, mas porque pus as mãos em leis matemáticas que já haviam sido descobertas por outros matemáticos antes de mim, a pé e da maneira certa. Para encorajamento, ele me enviou o livro Discrete Mathematics 1, no qual encontrei pela primeira vez os números de Stirling e Lach”, diz ele. O encorajamento, os elogios e a atitude de não subestimação do professor em relação ao menino de apenas doze anos encorajaram o menino a explorar mais.

Continuação na edição impressa ou aplicativo móvel de Nedeljski dnevnik